MLE와 MAP 그리고 딥러닝과의 관계에 대해...[1]

 

Likelihood (가능도, 우도)

- 입력으로 주어진 확률 분포(파라미터)가 얼마나 데이터를 잘 설명하는지 나타내는 점수

* 데이터를 잘 설명한다 -> 해당 확률 분포에서 높은 확률 값을 가지는 것을 의미한다.

 

어떠한 현상에 있어 확률 변수 x와 x의 확률의 곱의 합이 가능도가 된다. 

그러나 우리는 확률의 곱이 무수히 시행되면 그 값이 작아지게 되고 ( 분모가 무한대로 커지므로 ) 컴퓨터의

덧셈 연산의 장점을 위해 , 우도를 출력하는 함수에 log를 씌워서 log-likelihood로 변경한다. 

세타라는 파라미터를 가진 분포에서 x_i의 확률과 x_i들을 곱한 값의 합 = 우도

 

그렇다면 우리가 해야할 일은 위에 있는 log-likelihood를 가장 최대화 하는 세타θ  를 찾아야한다.

이때 어떠한 log-likelihood를 우도함수라고 한다면 이 함수는 위로 볼록한 함수이다. 

이때 최적의 파라미터 θ  는 gradient ascent로 찾아내게 된다. (아래로 볼록한 함수가 아니기 때문에) 

이 것을 우도를 최대한으로 하는 추정방법이라 하여 MLE(Maximum Likelihood Estimation)라고 하는데 

딥러닝의 관점에서 대부분의 딥러닝은 Gradient Descent를 지원하기 때문에  minimization 문제가 되고 

이를 위해 기존의 log-likelihood 에서 -를 붙여준 NLL(negative log-likelihood)가 되는 것이다.

또한 Gradient를 구하기 위해 log를 통해 곱셈의 문제를 덧셈으로 바꿔주면서 더 쉽게 미분이 가능하도록한다.  

 

즉 딥러닝 관점에서, 분포 P(x)로 부터 샘플링한 데이터 x가 주어졌을때, 파라미터θ 를 갖는 신경망은 조건부 확률 분포를 나타낸다. 

 

이때 Gradient Descent를 통해 NLL를 최소하하는 θ를 찾을 수 있게 된다. 

신경망 역시 확률 분포 함수이기 때문에 MLE- > NLL의 과정을 통해 파라미터를 찾는 것이라고 볼 수 있다. 

 

좀 더 수식의 관점에서 살펴보면 

우리가 찾는 최적 파라미터는 

다음과 같으며, 

이때 어떠한 확률분포 f(x) = f(y_iㅣx_i; θ)의 분포를

1) gausian distribution  2) bernoulli distribution

둘 중어느 분포로 가정하냐에 따라 위 손실함수는 MSE와 Cross-Entropy로 나뉘게된다. 

이는 아래와 같이 실제 가우시안 분포와 베르누이 분포에 식을 전개해보면 알 수 있다. 

출처 : https://www.youtube.com/watch?v=QfHcuPPW6W4&list=PLQASD18hjBgyLqK3PgXZSp5FHmME7elWS&index=6

 

즉 딥러닝의 대표 문제인  분류TASK에서  categorical한 분포를 가정하여 cross-entropy를 최소화하는 것을 MLE 관점으로 볼 수 있는 것이다.  

좌: NLL 우: CE

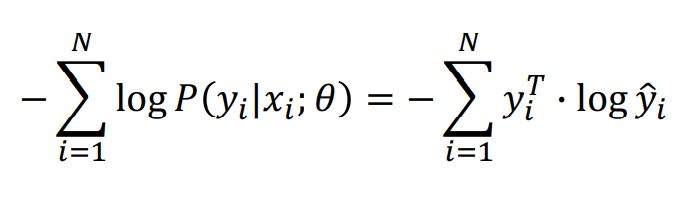
* 이때 보여지는 우변의 y_i는 one-hot encoding의 상태이기 때문에 [0,0,1,0,0,0..] 의 형태를 가지고 

y_hat은 좌변의 P(y_iㅣx_i; θ)와 같다. 

 

MLE와 MAP  그리고 딥러닝과의 관계에 대해...[2]

 

 

출처:

1. I. Goodfellow, Y. Bengio, A. Courville, “Deep Learning” (2015)