| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 빅쿼리
- spark #스파크
- 언어모델
- 빅쿼리 튜닝
- 도커오류
- spark explode
- tableau
- airflow
- 프로그래머스 파이썬
- 코테
- SparkSQL
- docker
- Big Query
- ifkakao2020
- 로컬 pyspark
- Docker error
- 데이터 시각화
- pyspark오류
- 도커exec
- LLM
- 데이터엔지니어링
- PySpark
- DataFrame Spark
- 시각화
- 도커
- spark df
- 태블로
- sparkdf
- BigQuery
- dataframe
- Today
- Total
SOGM'S Data
1) [논문리뷰] Collaborative Filtering for Implicit Feedback Datasets, IEEE 본문
1) [논문리뷰] Collaborative Filtering for Implicit Feedback Datasets, IEEE
왈왈가부 2020. 11. 2. 03:25Collaborative Filtering for Implicit Feedback Datasets, IEEE
<서론>
오늘 날 추천시스템의 가장 큰 줄기가 되는 MF기법중 사용자가 아이템에 남긴 평점(Explicit Datasets)이 아닌 Implicit Feedback Dataset을 이용하는 추천시스템이다.
우리 사회의 대부분의 비지니스는 고객이 어떤 물건에 평가하고 점수를 메기는 데이터를 가지고 있지않다. 즉, 대부분의 데이터는 사용자가 어떠한 item을 봤거나 , 구매 이력, 혹은 마우스 움직임까지 로그로 기록되어 있는 implicit data 이다.
이 논문은 implicit data를 다룰 때 explicit data를 다루는 알고리즘과 구분 짓기 위한 implicit data의 몇 가지 특징들을 다룬다.
1) 부정적인 피드백(data)는 없다(=알 수 없다).
- 어떠한 user가 아이템을 검색하지 않으면 그 값이 0이다. 이것은 user가 아이템을 관심이 없어서 검색하지 않은 것이 아닌 인지를 못한 것일 수 있다.
- 대부분의 explicit dataset을 다루는 recommender들은 0값을 , 선호하지 않는다고 판단하여 'missing data'로 간주하여 알고리즘에서 생략한다. 그러나 이 논문은 이러한 'missing data'가 data의 대부분이기에 이를 포함시켜 분석하는 법을 연구했다.
2) Implicit data는 본질적으로 noisy하다.
- user의 item의 value , 예를 들어 철수(user)가 온라인 쇼핑몰에서 볼펜(item) 판매 페이지에 체류한 시간(value)는 철수의 볼펜 사랑으로 볼 수도 있지만, 실은 단지 우연히 페이지가 열려있는 채 이를 잊고 다른 업무를 하는 바람에 쌓인 값일 수 도있다. 즉, 굉장히 변수가 많다.
3) Implicit data는 'confidence' 속성을 지닌다.
- explicit data가 평점과 같은 preference를 지니는 반면, implicit data는 사용자 행위의 빈도를 신뢰성(confidence)을 반영한다.
- 즉 large value가 높은 선호도가 아니다. -> 예를 들어, 이 논문에서의 예시 user들의 TV Programs(item)의 시청시간(value) 에서 오히려 선호도 높은 대작 영화는 2라는 value를 가지지만 설령 큰 값은 오랜 시간 방영하는 시리즈 물이다.
- 하지만 large value는 선호가 아닐 뿐 분명하고 유용한 데이터이기 때문에 confidence로 처리한다.
4) Implicit data은 적절한 평가지표가 필요하다.
- user가 본 TV program들 중 같은 시간에 상영하거나 , 한 번이상 watched 된 데이터가 존재한다. 이를 적절히 평가하기 위해서 그에 맞는 지표가 필요하다.
<본문>
<가정>
Implicit 을 다룰 때 no action을 뜻하는 0의 값들은 분석에 반드시 포함한다.
<이전 연구>
1) CF is based on Neighborhood models
- user-oriented 보다는 item-oriented가 'scalability' 와 'accuracy' 측면에서 더 좋음.
2) Latent Factor model
- SVD 기반 행렬 분해 ( USER-LATENT 행렬 * ITEM-LATENT 행렬)
* Typical model loss of Latent-Factor models( 람다 이하는 모델 발산 규제)

< Our Model >
- implicit dataset에 적절한 알고리즘
- loss함수

1. Cui: confidence(신뢰도) 로서 실제 value(rui) 에서, alpha값을 곱하여 1을 더해주는 값
- alpha는 논문 실험 결과 40이 가장 좋음.
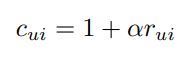
2. Pui: Action과 No action을 구분하는 binary 한 값.
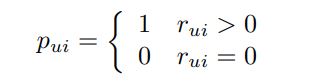
3. Lambda (λ) : 규제화 변수로서 cross_validation으로 결정됨.
< ALS > : Alternative Least Square
- 두 개의 행렬 X.T, Y의 내적으로 이뤄지기 때문에 SGD 방법은 Non-convex 문제가 된다. 따라서 X를 학습할 때 Y를 상수취급, Y를 학습할 때 X를 상수취급 함으로서 convex 문제로 바꾸기 위해 ALS를 사용한다.
* M명의 user, N개의 iTEM , MXN은 수 십억의 숫자가되며, SGD의 최적값 탐색을 방해(explicit dataset에서는 SGD가능)
- 손실함수를 X와 Y에 대해 각각 미분
( 예시 ) Loss함수를 X로 미분한 값이 0이 되는 값으로 update하는 과정.

위 사진은 손실함수로부터 행렬 X를 업데이트 한다.
* 행렬의 미분과 벡터의 미분을 신경써야 한다 개인적으로 가장 애먹었던 부분이다)
* 맨 아래 출처 참고.( 갈아먹는 머신러닝님의 블로그와 Stanford 자료)
즉 업데이트 된 Xu 는
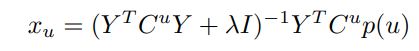
Yi 도 번갈아가면서 똑같이 업데이트 해주면 학습이 된다.
논문에 따르면 학습 ( typical number of sweeps ) 은 일반적으로 10번 이루어진다
<시간복잡도>
ALS는 explict dataset에서는 unknown data는 missing data로 취급하며 이뤄지지만 implicit dataset에서는 다른 접근이 필요하다. 그 접근은 변수 구조를 활용하여 als가 scalable 하게 작동하도록 한다.
과정은 다음과 같다.
1. 모든 user factor를 recomputing 한다.
2. item- factor 행렬을 n x f 라 하자.
3. 모든 user에 대해 반복적으로 돌기 전에 우리는 f x f 행렬 Y.TY를 계산하자 O(f^2n)
4. 모든 user u 에게 우리는 n x n 행렬인 대각 C_u를 정의하고 binary한 값으로 이루어진 vector P(P=Pui) 를 정의한다.
5. 컴퓨터적 bottleneck(병목화) 는 Y.T*Cu*Y를 구할때 발생한다.
-이를 위해 Y.T*Cu*Y = (Y.T*Y) + (Y.T*(Cu-i)*Y)로나눈다.
-앞 괄호는 아까 3에서 계산했다.
-뒤 괄호는 오직 n_u만큼만 non-zero를 가진다. 즉 r_ui>0보다 큰 dat만이므로 그러므로 데이터 개수는 n보다 작다.
- 즉, 시간복잡도 O(f^2n_u)
6. Cup(u) 도 마찬가지로 non-zero가 n_u만큼 있음. 시간복잡도 유지.
7. (Y.T*Cu*Y + λI) ^−1 역행렬 계산이 O(f^3)이다.
8. 이것은 모든 Xu에 대한식이며 모든 user에게 perform됨으로 total O(f^2n_u+f^3m)
중요한 것은 running time은 input_size와 선형적이다. 일반적인 f의 값은 20~200의 값이다.
반대로 yi의 경우 O(f2n_u +f^3m)
<추천을 설명하다>
이 논문의 알고리즘의 강점은 설명가능한 추천이다. 즉 왜 어떠한 user한테 특정 item이 좋은지를 나타낸다는 것이다.
기존의 neighborhood - based model들과 달리 latent factor model 들은 설명이 특히 까다로웠다. (모든 과거 유저들의 행동과 추천 결과의 관계가 user-factor들을 경유하여 추출되기 때문이다.
흥미롭게도 해당 논문의 알고리즘은 설명을 다음과 같은 방법으로 compute할 수 있다.
user u 의 item i 에 대한 preference 즉, new Pui = y.Ti * xu 이므로
new Pui= y.Ti (Y.T*Cu*Y + λI) ^−1 *YTCup(u) 로 표현할 수 있다.
(Y.T*Cu*Y + λI) ^−1를 Wu 라고 표현하면 ( 그리고 이것은 user u 에대한 가중치 매트릭스다 )
user u의 관점에서 item i, j 가중 유사도는 Suij = y.Ti*Wu*yj 이다.
즉, 새로운 식 (user u의 item i에 대한 예측된 선호도 값)은 다음과 같이 표현된다.

이것은 분리된 new_pi를 구함으로서 사용자의 이전 행동들의 공헌도를 가질 수 있게된다. 또한 사용자의 이전 행동을
1. user u - Cui의 관계의 중요성
2. item i - Suij의 유사성
두 가지로 구분짓게 된다.
<데이터 설명 및 전처리 >
[Train] = r_ui
1) 본 논문에 사용된 데이터는 300,000개의 셋탑박스에서 수집되었으며, item은 TV Program 17000 개 (i) , TV 시청 시간(value)으로 이루어져있다.
- 같은 프로그램의 중복 시청을 반영해보니 , non-zero value는 3200백만개이다.( 굉장히 sparse하다 )
[Test] = r_tui
1) 4주간 시청기록을 train data로 , 그 뒤 바로 따라오는 한 주를 test set으로 구성하였다.
- 논문에서 설명하길 tv 데이터 특성상 그 이상으로 길어지면 item이 바뀔 수 가 있다며 해당 기간에 타당성을 부여하는 설명을 추가했다.
2) TV 시청 데이터는 일주일마다 반복되어 시청하는 경향이 있으며 이러한 주기적인 시청의 영향을 데이터에서 제거한다.
- 한 번도 시청하지 않았던 프로그램이나 최근에 보지 않았던 프로그램을 추천하는게 훨씬 가치있기 때문이다.
- 각각의 유저들에게 Test data에 있는 item이 training 기간에도 시청되었다면 제거한다.
3) Test set에서 half 시간 이하로 본 데이터는 zero로 바꾼다.
- 유저가 좋아하는 프로그램이라 단정 짓기엔 약하다. r_tui<0.5
1~3)까지의 과정을 거친 r_tui의 non-zero는 약 200만개이다.
[scaling]
Log scaling 적용- 0부터 반복적으로 보는 tv 프로그램의 시청시간(over 10) 의 range를 좁히기 위해 정규화 해준다.
[그외 전처리]
TV를 채널 Tunning 후 program A를 시청한 후 A 다음의 방영되는 연속적인 prgram t, t+1, t+2... 에 대한 데이터가 있으면, 원해서 본 것이 아닌 계속틀어 놨을 확률이 높기에 down -weight 필요. 식은 아래와 같으며 a= 2, b=6이 일반적이다. t번째 program에대 한 가중치 . t=3일 경우 거의 r_ui 값이 반으로 줄어든다.

<평가함수>
1) 각 user별로 가장 덜 추천된 program 부터 가장 많이 추천된 program 까지 정렬된 리스트를 산출한다.
*단 implicit data는 비선호를 나타낼 수 없으며 모델의 추천에 대한 반응을 tracking 할 수 없다. 그러므로 precison 기반 지표가 아닌 recall 기반 지표를 써야한다.
precison = TP / TP + FP ( 예측 positve + 실제 positve / user가 positve하다고 예측 )
- 해당 모델에서 FP를 구할 수가 없음. FP는 모델이 user가 positive하다고 예측했지만 해당 예측이 실패한, 즉 실제로 Negative함을 증명해야하는데 implicit은 negative함을 나타낼 수가 없기 때문에.
recall = TP / TP + FN ( 예측 positve + 실제 positve / 실제 user가 positve )
- 즉 recall 기반 지표.
2) rank_bar 활용.
1)에서 봤듯이, recall 기반 즉, 실제 positive data를 이용한 지표인 rank_bar을 고안해내었다.
percentile ranking의 값을 활용한 rank_ui를 활용한다.
rank_ui는 한 user u 의 여러 개의 item i(배열)에 대한 percentail_rainking값이 배열로 저장 되어있다.
rank_ui = 0%라면 user u 에게 item i 는 가장 추천된 item을 뜻한다. 만약 50%라면 item i는 user u에게 중간정도로 추천된
item이다.
따라서 rank_bar의 식은 다음과 같다.

낮은 rank_bar의 값이 우수하다. user가 실제로 본 program과 추천된 program이 많이 일치한다. 참고로 난수 추천시스템 모델은 rank_bar의 값이 50%이다.
<평가 결과>
본 논문에서는 Our model의 factor의 수(f)를 10~200까지 시도했다. 또한 다른 2개의 모델과 경쟁 시켰다.
첫 번째 경쟁모델은 popularity 모델이다.
- program의 인기순대로 추천 결과를 정렬한 모델이다.
두 번째 경쟁모델은 neighborhood based(item-item) 모델이다.
- 모든 neighbor의 set을 이용했으며 cosine similarity를 사용했다.
결과는,
popularity 모델은 factor수와 관계없이 rank_bar가 약 16.46%
neighborhood based 모델은 factor 수와 관계없이 rank_bar가 약 10.74%
- popularity 모델은 아무런 자원의 소비없이 유의미한 값이 나왔지만, 이는 개인화 추천과는 거리가 멀다.
Our model은 facotr가 증가할수록 rank_bar가 줄어 들었으며 200일경우 8.35 값을 가졌다.
또한 상위 1%의 추천 program이 전체 test 시청 시간의 27%를 담당한다.
특히 <데이터 설명 및 전처리> 부분의
2) TV 시청 데이터는 일주일마다 반복되어 시청하는 경향이 있으며 이러한 주기적인 시청의 영향을 데이터에서 제거한다.
의 과정을 생략한다면 추천의 성능은 더욱 좋아진다.
=즉 Our model is the best.
평가 결과의 그 외의 사항으로는
1. Cui와 Pui로 나눠준 형태의 Ourt model은 기존 Latent model보다 훨씬 성능이 좋았다.
2. 규제화 λ = 150으로 수행했다.
3. Program들을 인기순으로 15등분했는데 인기있는 Program 집단일 수록 예측 성능이 좋았다.
- 즉, 인기 없는 프로그램을 추천하는 것이 어렵다.
- explicit data와 달리 데이터의 많고 적음이 예측성능에 영향을 덜 끼친다.
4. 모델의 설명성.
- 기존 latent 모델과 달리 추천의 설명이 가능하다.
- 아까 위에서 본, new_pi의 식에서 item간 유사도를 구할 수 있기 때문이다.
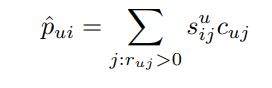
- 즉 어떠한 추천 program과 비슷한 program들의 목록을 알 수 있다.
- 대략적으로 TOP 5 similar programs 가 추천된 program의 약 35~40%를 설명한다.
<결론>
Our model은,
기존 latent model에서 r_ui 대신 Pui, Cui를 도입해서 모델의 성능을 좋게했다.
이 Pui, Cui는 사람들의 선호와 비선호를 명시하지 않는 implicit dataset에서 매우 유용하다.
또한 모든 data를 missingdata 까지도 모델에 반영할 수 있다.
모든 data를 다 반영하는 것은 확장성 측면에서 문제가 있다. 일반적으로 user들의 item에대한 availablity는 작기 때문이다. 따라서 이러한 문제점을 모델의 대수적 구조를 탐색하면서 해결한다. 위 <시간복잡도> 참고.
추천 결과에 대해 설명이 가능하다. neighborhood 방식으로 최근접 item을 보여주는 방식.
<향후 발전 방안>
zero data 끼리에서도 confidence를 나누는 방안을 고려.
user들의 not watch action에 대한 case연구
<+>
해당 논문은 scalability와 implicit dataset의 속성사이에서 적절한 밸런스를 맞춘 모델을 구현했다.
비록 ALS의 미분과 학습 과정이 조금 어려웠지만, 오늘 날 대다수의 데이터인 zero data들을 모델에 효율적으로 반영했다는 점에서 굉장히 흥미로웠다.
다음에는 해당 모델을 간단하게 구현해 볼 예정이다.
출처:
1. Y. Hu et al, Collaborative Filtering for Implicit Feedback Datasets
2. Matrix Completion via Alternating Least Square(ALS),stanford.edu/~rezab/classes/cme323/S15/notes/lec14.pdf
3. 갈아먹는 머신러닝 블로그, yeomko.tistory.com/4?category=805638
'About Data > AI Paper' 카테고리의 다른 글
| [PaperReview]SimCSE: Simple Contrastive Learning of Sentence Embeddings (1) (작성중) (1) | 2024.01.08 |
|---|---|
| [base] 내가 개인적으로 정리하는 중요 기초 논문 리스트 (0) | 2023.05.01 |
